You’ll likely encounter hyperkalemia on your next Resus / Cardiac shift, and you’ll instinctively treat it. But take a moment to review the fascinating physiology behind the “cocktail”! First, consider how K+ is buffered by cells: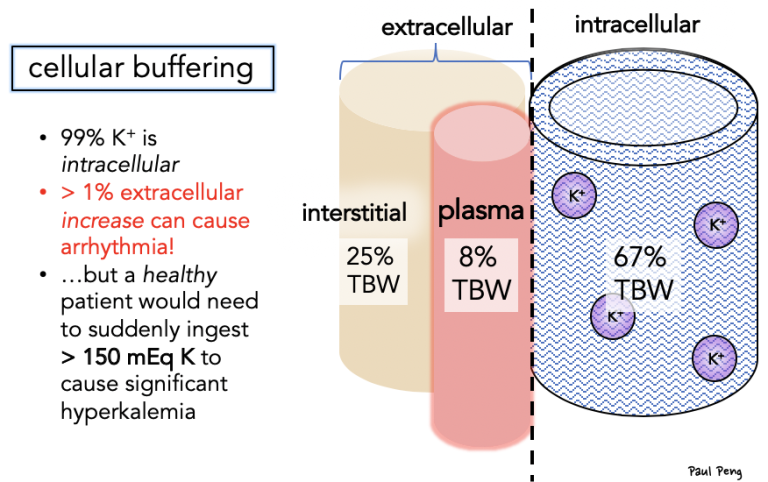
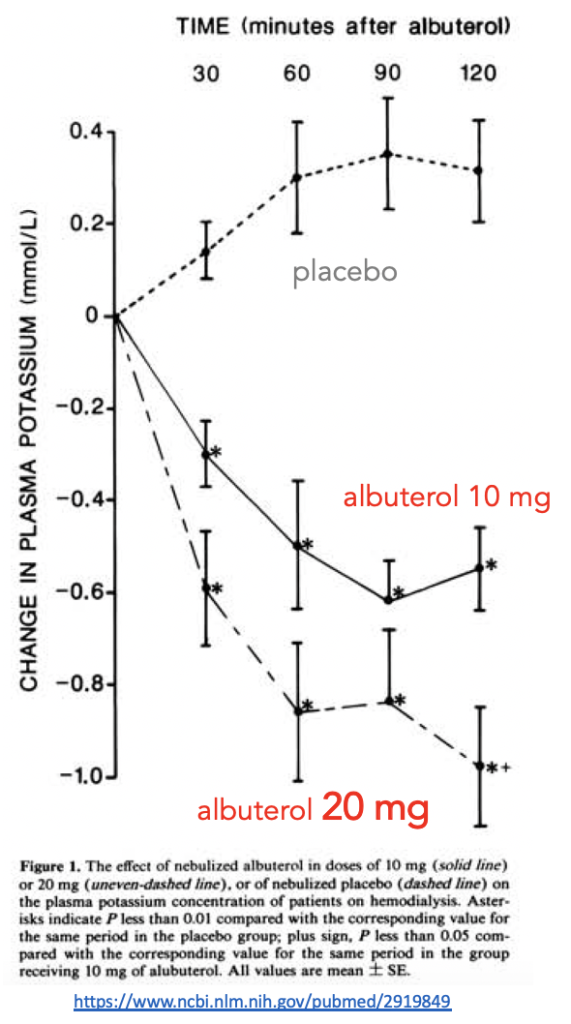
How do our treatments shift K+ intracellularly? … Key: Na-K-ATPase! 3Na+ out, 2K+ IN! And stimulated by the β2 and insulin receptors! Note how [3] acidemia affects K+ (shift out) and think about how that plays a role in DKA physiology.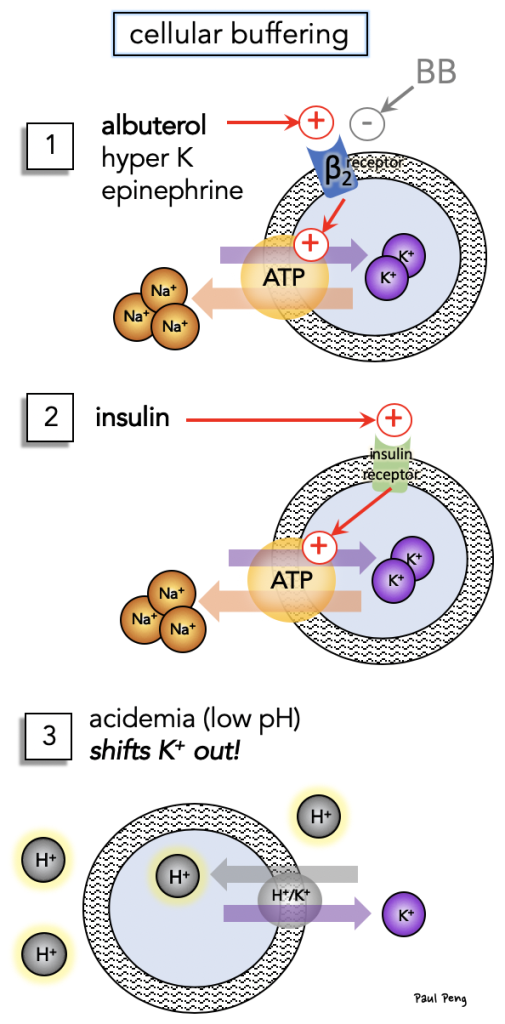
It may be a good idea to start a nebulizer treatment while the line is being placed because the effect is relatively fast… How fast? Check out the original literature below. NOTE: a common mistake is to dose the albuterol incorrectly.
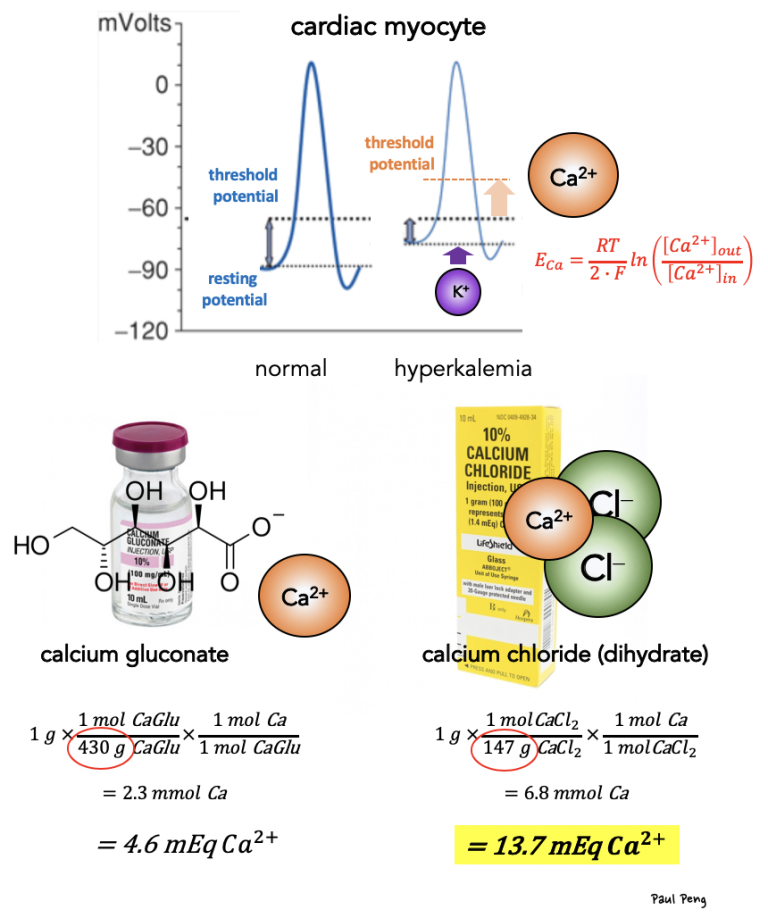
But you were probably thinking about calcium because of its “cardioprotective” effect. What is up with that? Cardiac myocte depolarization depends on extracellular K concentration (i.e. Nernst equation), and hyperK raises the resting potential closer to the threshold potential (i.e. more excitable). Calcium counters this by raising the threshold potential to mitigate excitability.
Gram for gram, calcium chloride contains 3X more mEq of calcium than calcium gluconate simply because gluconate is a relatively heavier molecule (i.e. in the denominator of the stoichiometry above!).
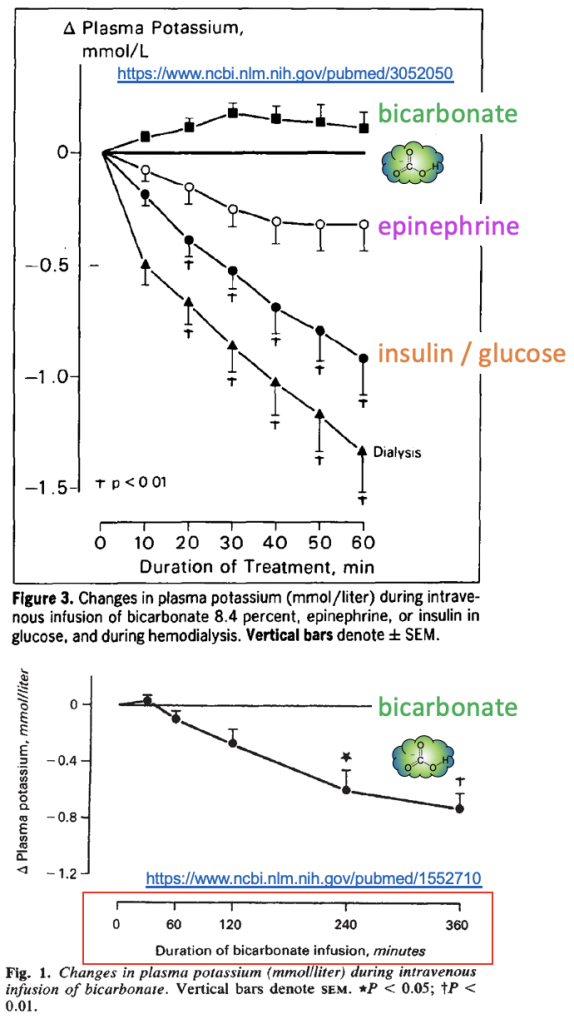
What about the rest of the treatments? Specifically, how fast will their effects take place?
- Bicarbonate takes much longer (I couldn’t find a good explanation)
- Insulin / dextrose is relatively fast (by 1 mM in 60 minutes!)
- NOTE: another pitfall is giving too much insulin (i.e. 10 U) to renal failure patients… use 5 U to prevent hypoglycemia
A future post will cover the RENAL HANDLING of potassium!
